Kapazitäts-Spannungs-Spektroskopie
Wenn sich ein extrinsischer Halbleiter in Kontakt mit einem Metall befindet, so bildet sich eine Verarmungszone aus, in der sich keine Ladungsträger befinden. Dieses System kann man zu Kapazitäts-Spannungs-Messungen (kurz: CV-Messungen) heranziehen, da man mit einer von außen angelegten Spannung die Verarmungszone vergrößern bzw. verkleinern kann. Die damit einhergehende Kapazitätsänderung kann dann dazu benutzt werden, um die im nachstehenden Abschnitt aufgelisteten Größen zu ermitteln.
Was erhalte ich durch Kapazitäts-Spannungsmessungen?
Durch Kapazitäts-Spannungs-Messungen kann man folgendes ermitteln:
- Donatorkonzentration
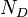 (
(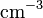 )
) - Diffusionsspannung (eingebautes Potential)
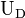 (V)
(V) - Verarmungslänge
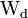 (nm)
(nm) - Bestimmung der Schottky-Barrieren-Höhe
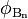
- Dotierprofil +++
- Ladungs- und Energiezustände von Quantenpunkten +++
Physikalischer Hintergrund
Die Kapazität in der Verarmungszone wird in Abhängigkeit der Spannung gemessen. Anders als bei einem Plattenkondensator befinden sich die Elektronen in der Metallschicht und die positiven Donatorionen in dem angrenzenden halbleitenden Volumen. Mit der Variation der angelegten Spannung kann die Breite der Verarmungszone verändert werden, was eine Änderung der Kapazität zur Folge hat. Bei homogener Dotierung hängt die Anzahl der Donatorionen linear mit der Breite der Verarmungszone zusammen, die wiederum mit der Wurzel des Potential bzw. mit der Spannung zusammenhängt. Es lässt sich folgende Gleichung herleiten:
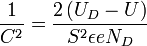
S ist hierbei die Kontaktfläche der aufgedampften Gates (für gewöhnlich 300 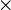 300 µ
300 µ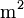 groß) und
groß) und  die Permittivität.
die Permittivität.
Trägt man nun 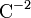 gegen die Spannung auf, kann man aus der Steigung der erhaltenen Geraden die Donatorkonzentration bestimmen:
gegen die Spannung auf, kann man aus der Steigung der erhaltenen Geraden die Donatorkonzentration bestimmen:
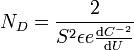
Ferner kann man aus dem Graphen die Diffusionsspannung 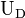 ermitteln, indem man den Spannungswert bei
ermitteln, indem man den Spannungswert bei 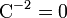 aus der Regressionsgeradenvorschrift errechnet.
aus der Regressionsgeradenvorschrift errechnet.
Möchte man sich den Verlauf der Verarmungslänge anschauen, so kann man die Beziehung für den Parallelplattenkondensator verwenden:
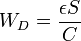
Die Schottky-Barrieren-Höhe kann dann mittels
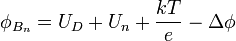
errechnet werden, wobei 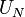 die Energiedifferenz zwischen Leitungsbandkante und Fermi-Level und
die Energiedifferenz zwischen Leitungsbandkante und Fermi-Level und 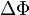 die Barrierenabsenkung aufgrund des Bildladungs-Effektes zwischen Flachband- und Null-Bias-Fall ist.
die Barrierenabsenkung aufgrund des Bildladungs-Effektes zwischen Flachband- und Null-Bias-Fall ist.